Longevity
Overview
The analysis of mortality and longevity has developed significantly over the last few years, and it is an area where I carry out much of my research. Some of this is outlined below, together with a broader description of the factors involved. First, though, it is important to distinguish between mortality and longevity risk. Mortality risk is the risk that mortality rates will be higher than expected; this is the risk faced by a life insurance company selling life insurance. Conversely, longevity risk is the risk that mortality rates will be lower than expected; this is the risk faced by a life insurance company selling annuities.
But there are actually several different types of mortality and longevity risk, and each requires a different treatment – though not all types apply to both mortality and longevity risk.
Components of mortality and longevity risk

Level Risk
Level risk is the risk that the estimate of the current underlying level of mortality is incorrect. For example, an insurance company might think that it is selling life insurance to office workers, and set the price accordingly. However, if it is actually selling policies to factory workers, then it might find that mortality rates – the probabilities of death at each age – are higher than it had expected.
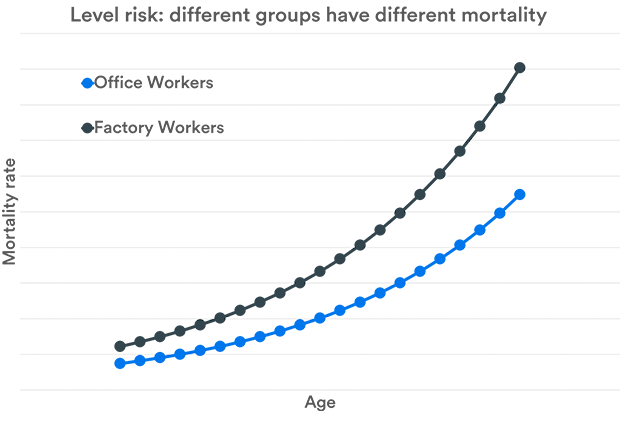
For individual policies such as life insurance, or even individual annuities, the level of risk is assessed – or underwritten – when the policies are sold. The same is true for some bulk insurance policies such as group life assurance. However, this is not the case for bulk annuities – that is, the transfer of defined benefit pension liabilities to insurance companies. Here, it is too late to get details directly from policyholders to help assess the risk.
One way to deal with this is to use what is known as “geodemographic profiling” – or postcode rating. This involves using where a person lives to give an indication of their life expectancy. To get more a more accurate indication of life expectancy this is best done indirectly, by looking at a range of characteristics that each location has, and determining the relationship between these characteristics and life expectancy. I have supervising a PhD thesis looking at this approach.
But even if you can estimate underlying mortality rates in this way, each individual – and thus each group of individuals – is unique. This means that the best way to judge mortality rates for a group is to look at the past mortality experience of that group. The challenge here is that you need a large number of individuals to come up with reliable estimates. As such, it is necessary to find a way to combine estimates from past experience with estimates from approaches such as postcode rating. This is known as credibility theory, with more weight – or credibility – being given to the experience-based results the larger the experience is. This is typically carried out using mortality rates at each individual age. However, it is possible to work the experience data a little harder – as I show in this paper.
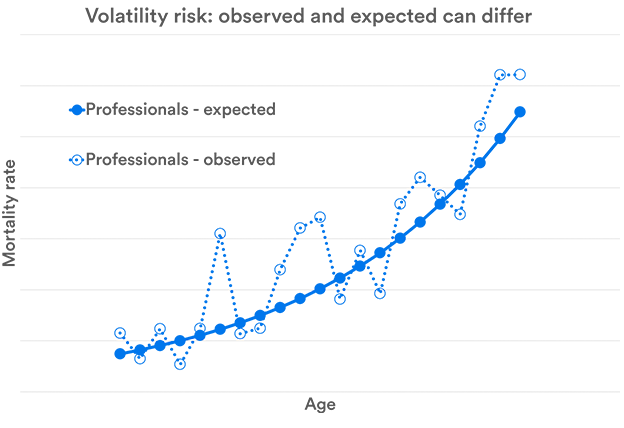
Volatility Risk
Even if the underlying level of mortality has been correctly estimated, it is still difficult to estimate the exact number of deaths. For example, if your model predicts 13.5 deaths in a year, you can be pretty sure that it will be wrong – half a death is rather unlikely. This issue is important for small defined benefit pension schemes, where this volatility can lead to a significantly higher level of risk – the risk being that the pensions will not ultimately be paid. This risk forms part of the research I am carrying out into pension scheme funding.
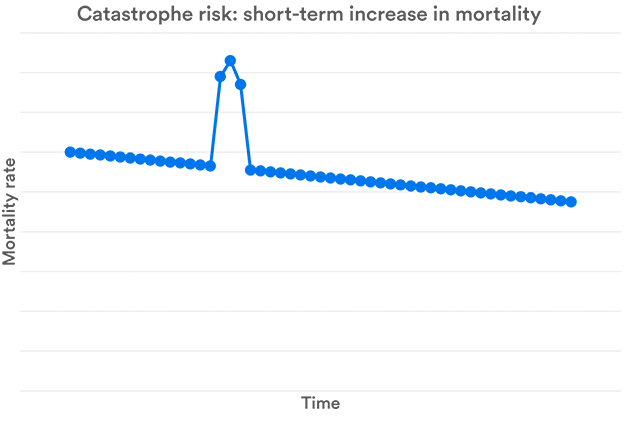
Catastrophe Risk
Catastrophe risk could be thought of as an extreme form of volatility risk. However, whilst deaths are independent for volatility risk, they are somehow linked for catastrophe risk. Catastrophe risk is relevant only for mortality. It occurs when there is a large but temporary increase in the number of deaths. This is typically due to war, pandemics or some other natural disaster. However, a longevity version of catastrophe risk – which would see a large, temporary drop in the number of deaths is not likely – unless it is due to volatility, in which case it is described as volatility risk.
Trend Risk
All of the risks discussed so far focus on current levels of mortality rates. However, for institutions such as pension schemes, future mortality rates are a major issue. To work out what mortality rates will be in the future, some sort of projection is required – and the risk of getting this wrong is trend risk.
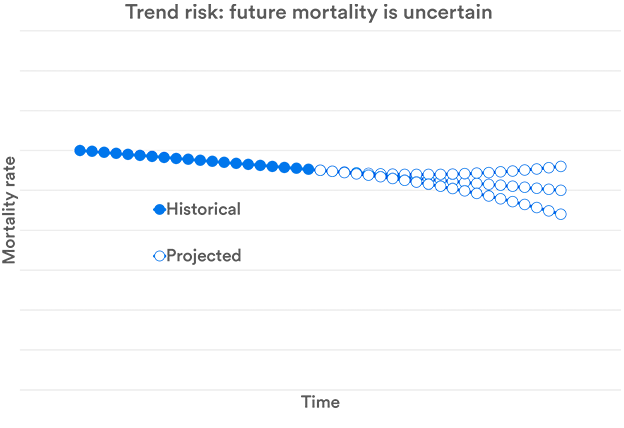
There are a number of approaches that can be used to forecast mortality rates. Some look at causes of death, others at risk factors. However, it is difficult to assess the level uncertainty in these projections. A simpler strategy is simply to identify patterns in historical rates and use these to assess both expected longevity and the risk associated with these estimates.
Much of my research has been in this area. Some of the work is aimed at simplifying mortality projections, such as this paper. However, I also look at the patterns that mortality projections could be expected to follow, as explained in this paper. In simple terms, this suggests that there is much greater uncertainty over long-term mortality and longevity forecasts than implied by many models.
Another area I consider is the cohort effect. This is the influence that year of birth has on mortality rates, over and above the influence of age and calendar year. Mortality rates generally increase with age. They also generally fall over time. However, there are some cohorts – populations with a common year of birth – whose mortality improves at a different rate to earlier or later cohorts. Research such as this looks at alternative ways of modelling the cohort effect using fewer parameters.